并行计算MPI 埃拉筛及性能优化

Posted Mar 31, 2024 Updated Apr 13, 2024

By Akejyo 47 min read

分布式并行计算 lab1

埃拉托斯特尼素数筛选算法并行及性能优化

实验目的

使用 MPI 编程实现埃拉托斯特尼筛法并行算法。
对程序进行性能分析以及调优。基础有三个优化：
- optimize1 去掉偶数；
- optimize2 消除广播；
- optimize3 Cache 优化。
最后还需自行实现 optimize4 来尽可能的去优化，但是不能开 O2 、改算法等。

实验环境

华为云弹性服务器，规格/镜像：

_鲲鹏通用计算增强型 2vCPUs 4GiB kc1.large.2_ > Ubuntu 18.04 server 64bit with ARM(40GiB)

实验过程

$\boxed{\text{base}}$：普通的 MPI 埃拉筛

在进行并行算法和这么多优化之前，首先需要理解埃拉筛的实现原理：

对于任意一个大于 $1$ 的正整数 $n$，它的 $x$ 倍一定是个合数（$x>1$）。从小到大考虑每个数字 $a$，把 $a*x$ 全部标记为合数，没有标记到的就是素数。

串行实现埃拉筛十分简单，在此基础上使用 MPI 并行算法也很容易理解：

假设我们有 $p$ 个进程，则将 $n$ 个数分成 $p$ 块，每个进程只处理自己对应范围的数，具体一点为：对于进程 $i$ ，它处理的数的范围下界为 $\lfloor in/p\rfloor$，上界为 $\lfloor (i+1)n/p\rfloor-1$。
考虑到数字 $0$ 和 $1$ 是不需要处理的，我们处理数据实际上是从 $2$ 开始，上下界在代码里是 low_value = 2 + i * (n - 1) / p; 和 high_value = 1 + (id + 1) * (n - 1) / p;
每个进程要处理的事，就是先取一个前面筛好的素数 $prime$，找到这个素数第一次出现在自己所负责区间的一个倍数 $first$，不断的将 $first$ 加 $prime$ 来标记合数，标记完这个区间后再取下一个素数。
每个进程需要使用的素数来自第一个进程的广播。进程 $0$ 号筛选初始素数，每筛选出来一个新的素数就广播给其他所有进程。
在标记合数部分，数组的大小只需要开到每个区间的大小即可，可以将 $first$ 映射到这个数组里：
- 若 $prime^2 > low_{value}$ ($low_{value}$ 是这个进程处理区间的下界)： $first = prime^2 - low_{value}$
  取 $prime^2$ 作为第一个要映射到数组的解释如下：设 $prime^2$ 的前一个 $prime$ 的倍数为 $prime*a$，$a$ 一定小于 $prime$
  - 如果 $a$ 是质数，由于我们用来筛选的素数是从小到大的，$a$ 一定已经使用过了，$prime*a$ 也一定已经被标记过了；
  - 如果 $a$ 不是质数，将 $a$ 质因数分解，因为 $a<prime$，所以 $a$ 的质因子一定小于 $prime$ ，那么就一定是已经使用过的素数，$prime*a$ 是被标记过的。
- 若 $prime^2 \le low_{value}$：
  - 若 $low_{value}\mod prime = 0$ $first = prime-(low_{value}\mod prime)$
  - 否则 $first=0$ 。

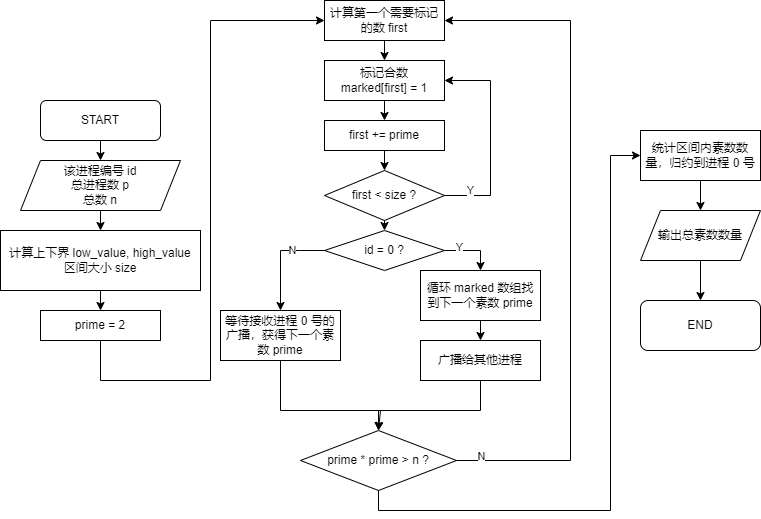
`base.cpp` 程序框图：

`base.cpp` 程序运行结果：

进程数	运行时间
1	$110.5$ s
2	$62.2$ s
4	$62.5$ s
8	$61.6$ s
16	$58.1$ s

观察随着进程数量增加，运行需要的时间减少的幅度逐步变小，推测与通信效率有关。另外由 Amdahl 定律，并行程序的加速比受可并行部分的限制，而这个 base.cpp 的并行部分有很大的优化空间。

$\boxed{\text{optimize1}}$：去除偶数

显然偶数都不是素数，可以提前去除所有偶数来减半问题规模。与 base.cpp 的区别是：

区间大小只需之前的一半，用来标记合数的 marked 数组也只需要之前一半的大小。

取 $first$ 部分，考虑到我们的 marked 数组大小减半了，需要多考虑一些因素来映射，总体思路不变，可见代码：

  
if (prime * prime > low_value)
    first = (prime * prime - low_value) / 2; // 减半
else {
    if (!(low_value % prime))
        first = 0;
    else if (low_value % prime % 2 == 0)
        first = prime - ((low_value % prime) / 2);
    else
        first = (prime - (low_value % prime)) / 2;
}

上述代码最需要解释的部分是 $low_{value}\ \% \ prime$ 是偶数的部分：

由于 $low_{value}\ \% \ prime$ 是偶数，那么 $primea-low_{value}$ 一定是个奇数（ $primea$ 是第一个大于 $low_{value}$ 的 $prime$ 的倍数），又因为我们不考虑所有偶数，$low_{value}$ 必定是奇数，所以 $primea$ 就必定是偶数，需要排除这个。因此实际上我们是用 $2prime$ 来找下一个合数，而这个合数一定是需要标记的奇合数。

`optimize1.cpp` 程序框图：

optimize1.cpp 程序框图与 base.cpp 结构相同，可见 base.cpp 的程序框图。需要注意 $prime$ 初始为 $3$ 而不是 $2$。

`optimize1.cpp` 运行结果：

进程数	运行时间
1	$52.6$ s
2	$29.7$ s
4	$29.6$ s
8	$27.8$ s
16	$29.6$ s

与 base.cpp 对比可以看到，时间差不多缩短了一半，说明去除偶数对效率的提升非常直接有效。

$\boxed{\text{optimize2}}$：消除广播

注意到每个进程使用的素数都是从进程 0 广播得到的，而这个广播是完全可以消除掉的。每个进程自己找自己需要的素数，筛选 $n$ 范围的数最大只需要 $\sqrt n$ 的素数。使用串行算法获得 $\sqrt n$ 范围的素数，就不需要等待广播了。

至于如何筛选 $\sqrt n$ 范围的素数，我选择使用欧拉筛，时间复杂度只有 $O(n)$ 且简单好写. 该算法最核心的部分在于：对于一个数 $i$，在筛 $i*prime$ 的过程中，如果遇到 $i\ \%\ prime=0$ 的情况就直接跳出当前循环。

由于 $prime$ 是从小到大筛选出来的，$i$ 乘其他质数的一个合数一定会被 $prime$ 的倍数筛掉，例如设 $i=2\times 3=6$，$prime=2$，下一个素数是 $3$，$i*3=18$，会发现 $18$ 一定会被 $i=9,prime=2$ 的情况筛掉.

  
    vector<int> pri;
    int pri_i = 1;
    int sqrt_N = sqrt(n) + 10;
    bool not_prime[sqrt_N + 10] = {0};
    for (int i = 2; i <= sqrt_N; i++) {
        if (!not_prime[i]) pri.push_back(i);
        for (int prime_i : pri) {
            if (i * prime_i > sqrt_N) break;
            not_prime[i * prime_i] = true;
            if (i % prime_i == 0) break; //直接 break
        }
    }

`optimize2.cpp` 程序框图：

提前筛选 $\sqrt n$ 的素数，不从进程 $0$ 获得下一个素数而是从自己的获得。

`optimize2.cpp` 运行结果：

进程数	运行时间
1	$52.7$ s
2	$29.3$ s
4	$29.0$ s
8	$27.4$ s
16	$25.8$ s

与 optimize1.cpp 对比，差异主要体现在进程数为 $16$ 的时候，说明进程数越多，消除通信带来的加速就越明显。

$\boxed{\text{optimize3}}$ Cache 优化

cache 是一种小型快速内存，访问 cache 中的数据速度远超访问普通内存的数据。如果我们能尽可能的在同一个 cache size 里处理数据，那么 cache 命中率就会提高，整体速率就会提高。对于数组这样的数据，每当我访问一个数据元素时，缓存会存储数组一个 cache line 大小的数据以便后续使用。

我们还发现，在用相近的素数进行筛选时，它们在一定范围内经常会筛到同一个合数，结合刚才对 cache 的描述，接下来要做的就是按照 cache size 对进程需要处理的数据重新分块。

如何计算分块的数据范围大小，我是这样计算的：

首先需要知道 cache size，输入以下指令 lscpu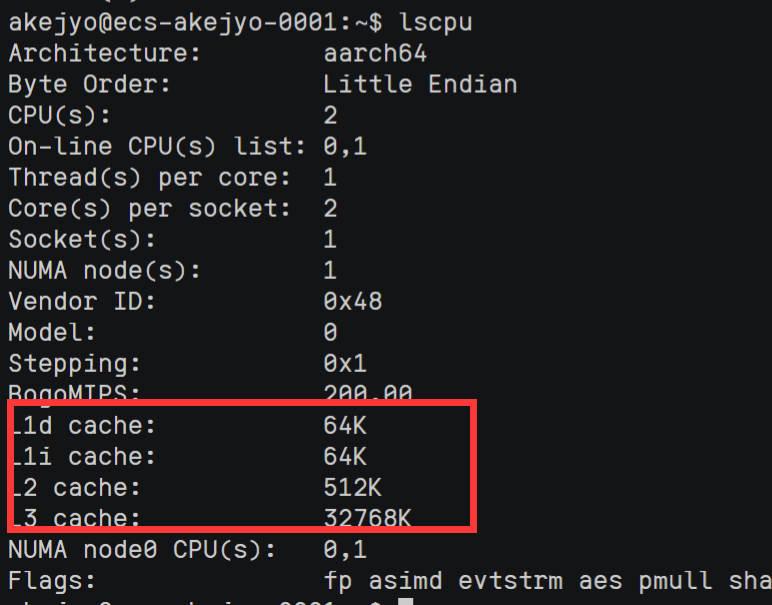 使用 L3 缓存，cache size 大小为 $32768*1024=33554432\ B$。
以最终测试标准 $8$ 个进程来计算，首先 cache size 平分给 $8$ 个进程，此时得到 $33554432/8=4194304\ B$ ，考虑到缓存的冗余，选择使用缓存的 $1/4$ 大小使用，即 $1048576\ B$。
再考虑代码细节，有一个 char 类型数组作标记用，一个 long long int 类型数组存储用来筛选的素数，这个素数数组最大是 $\sqrt n$，粗略计算就是 $x$ 个 char 数据是和 $\sqrt x$ 个 long long int 数据绑定在一起的，也就是平均每个数据大小 $1(sizeof\ char)+\sqrt{8(sizeof\ long\ long\ int)}\approx4\ B$。
最后算得 $Block_{size}=1048576/4=262144\ B$。
总结一下就是 CACHE_SIZE / p / 4 / 4，我尝试了多种计算方式和多种大小，最后发现这样做似乎效果不错，就这样用下来了。

接下来是每个块的处理，其实与前面还是很类似，如同套娃一般分块再分块，每次我们都需要计算这个块的上下界，然后进行筛选和统计。

程序需要处理的数据量：N = (n - 1) / 2 块的数量（从 0 开始）：Block_N = CacheBlock_size - 1
该进程第一个数的索引：low_index = id * (N / p) + MIN(id, N % p) 该进程最后一个数的索引：high_index = (id + 1) * (N / p) + MIN(id + 1, N % p) - 1
该进程下界：low_value = low_index * 2 + 3 该进程上界：high_value = (high_index + 1) * 2 + 1
块中第一个数的索引：Block_first = Block_id * Block_N + MIN(Block_id, Block_rest) + low_index 块中最后一个数的索引：Block_last = (Block_id + 1) * Block_N + MIN(Block_id + 1, Block_rest) - 1 + low_index
块的下界：Block_low_value = 2 * Block_first + 3 块的上界：若不是最后一个块则为 Block_high_value = 2 * Block_last + 3；否则为 Block_high_value = high_value
接下来的处理和前面类似，当 $prime^2\gt Block_{high\ value}$ 时退出当前循环。

`optimize3.cpp` 程序框图：

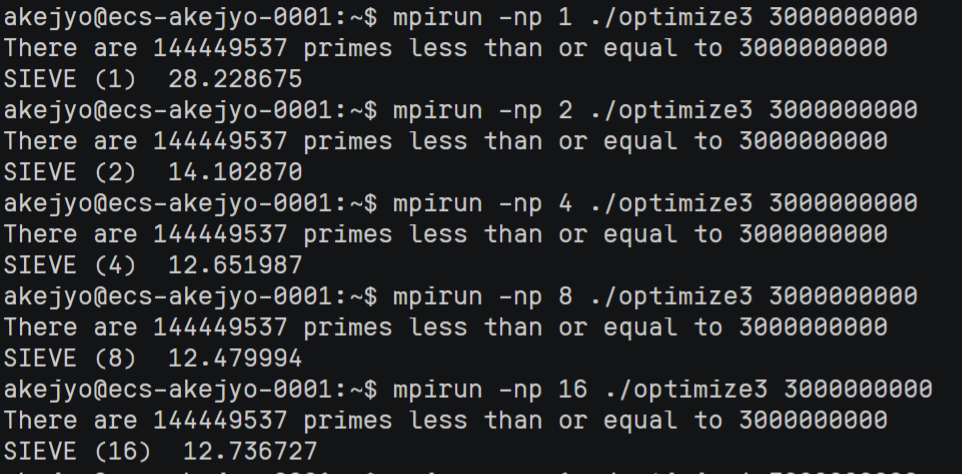
`optimize3.cpp` 运行结果：

进程数	运行时间
1	$28.2$ s
2	$14.1$ s
4	$12.7$ s
8	$12.5$ s
16	$12.7$ s

与 optimize2.cpp 对比，加速效果显著，cache 的存取效率确实是非常优秀。

$\boxed{\text{optimize4}}$ 最终优化

这部分优化基本自由发挥了，我将大致按时间顺序介绍我的优化流程. 需要注意的是，下面的优化在调试时使用的参数大多为 $16$ 进程数，数据量 $3e9$.

使用 memset 替换 for 循环初始化 marked 数组
memset(marked,0 , CacheBlock_size);
效果显著，从 $12.7$s → $9.7$s

循环展开

由于循环体包含了循环条件等分支预测，在一次循环里处理多次数据可以减少分支预测错误.

  
for (i = first; i < CacheBlock_size; i += 4*prime) {
    marked[i] = 1;
    if (i + prime < CacheBlock_size) marked[i + prime] = 1;
    if (i + 2*prime < CacheBlock_size) marked[i + 2*prime] = 1;
    if (i + 3*prime < CacheBlock_size) marked[i + 3*prime] = 1;
}

这里我一次循环标记了 $4$ 个 marked 数组，时间来到 $7.7$s

同理还可以处理统计数量的那个循环：

  
    for (i = 0; i < CacheBlock_size; i += 4) {
        if (!marked[i]) count_cacheBlock++;
        if (i + 1 < CacheBlock_size && !marked[i + 1]) count_cacheBlock++;
        if (i + 2 < CacheBlock_size && !marked[i + 2]) count_cacheBlock++;
        if (i + 3 < CacheBlock_size && !marked[i + 3]) count_cacheBlock++;
    }

→ $6.1$s

关于上面这个循环，里面有太多的 if 语句，循环展开需要的就是减少分支预测，稍微修改一下结构和 merked 的值：

  
        for (i = 0; i < CacheBlock_size; i += 4) {
            count_cacheBlock0 += marked[i];
            if (i + 3 < CacheBlock_size) {
                count_cacheBlock1 += marked[i + 1];
                count_cacheBlock2 += marked[i + 2];
                count_cacheBlock3 += marked[i + 3];
            } else if (i + 2 < CacheBlock_size) {
                count_cacheBlock1 += marked[i + 1];
                count_cacheBlock2 += marked[i + 2];
            } else {
                count_cacheBlock1 += marked[i + 1];
            }
        }

这里我将 marked 改成初始化为 $1$，标记合数为 $0$，因此直接统计上就行. → $5.3$s

使用 `__builtin_popcountll` 函数来统计

__builtin_popcountll 是 GCC 编译器提供的一个内建函数，用于计算一个 unsigned long long 类型的数值中二进制表示下的 1 的个数，也就是所谓的汉明权重（Hamming Weight）。

  
tmpSize = (CacheBlock_size >> 6) << 6;
for (i = 0; i < tmpSize; i += 64) {
    count_cacheBlock0 += __builtin_popcountll(*((unsigned long long *)(marked + i)));
    count_cacheBlock1 += __builtin_popcountll(*((unsigned long long *)(marked + i + 8)));
    count_cacheBlock2 += __builtin_popcountll(*((unsigned long long *)(marked + i + 16)));
    count_cacheBlock3 += __builtin_popcountll(*((unsigned long long *)(marked + i + 24)));
    count_cacheBlock4 += __builtin_popcountll(*((unsigned long long *)(marked + i + 32)));
    count_cacheBlock5 += __builtin_popcountll(*((unsigned long long *)(marked + i + 40)));
    count_cacheBlock6 += __builtin_popcountll(*((unsigned long long *)(marked + i + 48)));
    count_cacheBlock7 += __builtin_popcountll(*((unsigned long long *)(marked + i + 56)));
}
count += count_cacheBlock0 + count_cacheBlock1 + count_cacheBlock2 + count_cacheBlock3 + count_cacheBlock4 + count_cacheBlock5 + count_cacheBlock6 + count_cacheBlock7;
for (; i < CacheBlock_size; i++)
    count += marked[i];

这里使用 __builtin_popcountll 每次统计了 $8$ 位 marked 数组的值，一次循环就统计了 $64$ 个值，效率上升显著. 由于这种处理方式可能会越界，所以先将 CacheBlock_size 末 $6$ 位消掉，分开独立处理.

→ $4.3$s（数据因为忘记重置计数了导致结果不对，但是时间不会有影响）

继续减少标记 `marked` 数组部分的分支判断

想办法得到一个不会越界的大小，分开处理数据：

  
tmpSize = CacheBlock_size - (CacheBlock_size - first) % (prime << 2);
for (i = first; i < tmpSize; i += (prime << 2)) {
    marked[i] = 0;
    marked[i + prime] = 0;
    marked[i + (prime << 1)] = 0;
    marked[i + 3 * prime] = 0;
}
for (; i < CacheBlock_size; i += prime) marked[i] = 0;

→ $3.5$s

增加标记 `marked` 数组的循环展开常数

本来是一次处理 $4$ 个数据，改为一次处理 $8$ 个数据

  
tmpSize = CacheBlock_size - (CacheBlock_size - first) % (prime << 3);
for (i = first; i < tmpSize; i += (prime << 3)) {
    marked[i] = 0;
    marked[i + prime] = 0;
    marked[i + (prime << 1)] = 0;
    marked[i + 3 * prime] = 0;
    marked[i + (prime << 2)] = 0;
    marked[i + 5 * prime] = 0;
    marked[i + 6 * prime] = 0;
    marked[i + 7 * prime] = 0;
}
for (; i < CacheBlock_size; i += prime) marked[i] = 0;

稍微快了一点，→ $3.3$s，其实这个级别的变化有可能是普通的波动，但至少没有出现负优化。

杂七杂八的优化
- 指针操作
  1 2 3 4 5 char *mark = marked + i; *mark = 0; *(mark + prime) = 0; *(mark + (prime << 1)) = 0; ...
- 多用二进制运算，如 %2 用 &1 替换，位运算的效率远快于普通运算。
- 使用 __builtin_expect 函数，这个函数是帮助编译器做分支预测的，我在一些分支选择多的地方先统计各分支的数量，根据结果将分支条件添加 likely(x) 或 unlikeky(x)。花了很多工夫，但效果一般。
  1 2 #define likely(x) __builtin_expect(!!(x), 1) #define unlikely(x) __builtin_expect(!!(x), 0)
- 减少 Block_low_value % prime，设置一个变量来记录。这个表达式多次出现在循环主体里，减少计算次数后速度有所上升。
- 调整了 CacheBlock_size 大小，具体可见 optimize3 的介绍该步优化提升显著.

使用 `register` 关键字 & 内联汇编

register 是用于提示编译器尽可能将变量存储在 CPU 寄存器中以提高访问速度的关键字，这个优化我本来是没有保有希望，考虑到 register 关键字已经被废弃，现代编译器会直接把这个关键字忽略掉，但很神奇的是起效了。我在多次尝试后决定将循环体使用到的变量全部加上 register 关键字，在 $8$ 进程、数据量 $4e9$ 的参数下加快了 $1$s 左右，真的是很大的一步。在此之前我尝试了很多奇奇怪怪的思路，都很难有突破。

我查到 register 是在 C++11 及以后的版本 deprecated，在 C++17 被 removed，看一下平台的 mpic++ 版本

Using the GNU Compiler Collection (GCC): C Dialect Options 可以查到 g++ 7.5 默认使用 C++14：

GNU dialect of -std=c++14. This is the default for C++ code.

在 Using the GNU Compiler Collection (GCC): C++ Dialect Options 可以查到有关 register 关键字的信息：

Warn on uses of the register storage class specifier, except when it is part of the GNU Explicit Register Variables extension. The use of the register keyword as storage class specifier has been deprecated in C++11 and removed in C++17. Enabled by default with -std=c++1z.

代码里的变量应该都是 local variables，继续进入网址 Using the GNU Compiler Collection (GCC): Local Register Variables 。这里详细介绍了怎么使用 register 才有效的介绍，说到必须用 asm 来指定寄存器，还要用上内联汇编。

  
register int *p1 asm ("r0") = …;
register int *p2 asm ("r1") = …;
register int *result asm ("r0");
asm ("sysint" : "=r" (result) : "0" (p1), "r" (p2));

参考标准写法，下面是我把标记 marked 数组部分改成内联汇编的代码，保留了循环展开：

  
    register bool *tmp_marked asm("x7");
    register unsigned LL tmp_i asm("x9");
    register unsigned LL tmp_prime asm("x10");
    register unsigned int zero asm("w8");

            tmpSize = CacheBlock_size - (CacheBlock_size - first) % (prime << 3);
            i = first;
            tmp_marked = &marked[0];
            tmp_i = (unsigned LL)i;
            tmp_prime = (unsigned LL)prime;
            zero = 0;
            asm volatile(
                "2:\n"
                "cmp x9, %2\n"       // i < tmpSize?
                "bge 1f\n"
                "strb w8, [x7,x9]\n" // marked[i] = 0
                "adds x9, x9, x10\n" // i+=prime
                "strb w8, [x7,x9]\n"
                "adds x9, x9, x10\n"
                "strb w8, [x7,x9]\n"
                "adds x9, x9, x10\n"
                "strb w8, [x7,x9]\n"
                "adds x9, x9, x10\n"
                "strb w8, [x7,x9]\n"
                "adds x9, x9, x10\n"
                "strb w8, [x7,x9]\n"
                "adds x9, x9, x10\n"
                "strb w8, [x7,x9]\n"
                "adds x9, x9, x10\n"
                "strb w8, [x7,x9]\n"
                "adds x9, x9, x10\n"
                "b 2b\n"
                "1:\n"
                : "+r"(tmp_i)
                : "r"(tmp_marked), "r"(tmpSize), "r"(zero)
                : "cc", "memory");
            i = tmp_i;
            for (; i < CacheBlock_size; i += prime) marked[i] = 0;

速度稍微快了点，到 $2.7$s

关于统计 marked 数组中 $1$ 的数量，我尝试了一下用内联汇编替代，但效果不甚理想，可能本来用 __builtin_popcount 就够快了，也可能是我汇编写不到位。

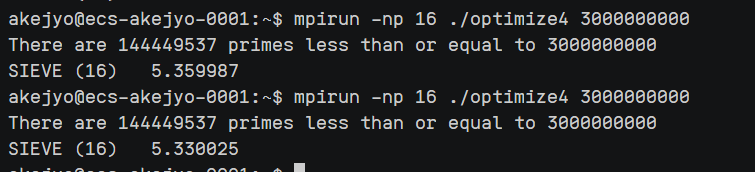
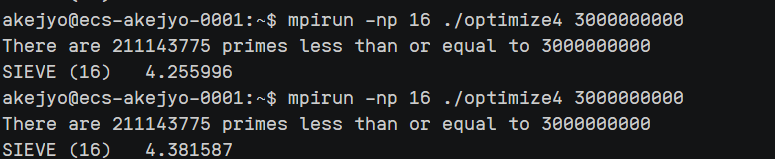
`optimize4.cpp` 运行结果：

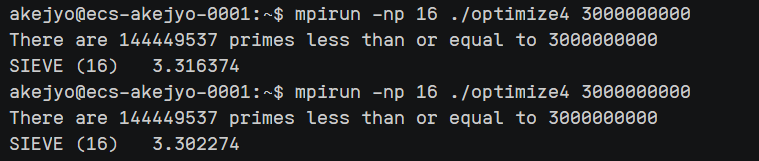
进程数量 $1$ 到 $16$，数据量 $3e9$：

进程数	运行时间
1	$5.4$ s
2	$3.3$ s
4	$1.9$ s
8	$2.0$ s
16	$2.1$ s

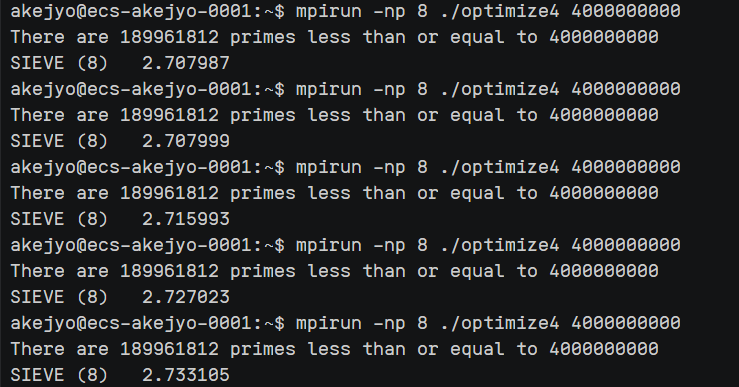
最终测评参数，进程数量 $8$，数据量 $4e9$

代码

`base.cpp`

  
#include "mpi.h"
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define MIN(a, b) ((a) < (b) ? (a) : (b))
#define LL long long

int main(int argc, char *argv[]) {
    LL count;            /* Local prime count */
    double elapsed_time; /* Parallel execution time */
    LL first;            /* Index of first multiple */
    LL global_count = 0; /* Global prime count */
    LL high_value;       /* Highest value on this proc */
    LL i;
    int id;              /* Process ID number */
    LL index;            /* Index of current prime */
    LL low_value;        /* Lowest value on this proc */
    char *marked;        /* Portion of 2,...,'n' */
    LL n;                /* Sieving from 2, ..., 'n' */
    int p;               /* Number of processes */
    LL proc0_size;       /* Size of proc 0's subarray */
    LL prime;            /* Current prime */
    LL size;             /* Elements in 'marked' */

    MPI_Init(&argc, &argv);

    /* Start the timer */

    MPI_Comm_rank(MPI_COMM_WORLD, &id);
    MPI_Comm_size(MPI_COMM_WORLD, &p);
    MPI_Barrier(MPI_COMM_WORLD);
    elapsed_time = -MPI_Wtime();

    if (argc != 2) {
        if (!id) printf("Command line: %s <m>\n", argv[0]);
        MPI_Finalize();
        exit(1);
    }

    n = atoll(argv[1]);

    /* Figure out this process's share of the array, as
        well as the integers represented by the first and
       last array elements */

    low_value = 2 + id * (n - 1) / p;
    high_value = 1 + (id + 1) * (n - 1) / p;
    size = high_value - low_value + 1;

    /* Bail out if all the primes used for sieving are
       not all held by process 0 */

    proc0_size = (n - 1) / p;

    if ((2 + proc0_size) < (int)sqrt((double)n)) {
        if (!id) printf("Too many processes\n");
        MPI_Finalize();
        exit(1);
    }

    /* Allocate this process's share of the array. */

    marked = (char *)malloc(size);

    if (marked == NULL) {
        printf("Cannot allocate enough memory\n");
        MPI_Finalize();
        exit(1);
    }

    //!------这里也许可以用 memset
    for (i = 0; i < size; i++) marked[i] = 0;
    if (!id) index = 0;
    prime = 2;
    do {
        if (prime * prime > low_value)
            first = prime * prime - low_value;
        else {
            if (!(low_value % prime))
                first = 0;
            else
                first = prime - (low_value % prime);
        }
        for (i = first; i < size; i += prime) marked[i] = 1;
        if (!id) {
            while (marked[++index])
                ;
            prime = index + 2;
        }
        if (p > 1) MPI_Bcast(&prime, 1, MPI_INT, 0, MPI_COMM_WORLD);
    } while (prime * prime <= n);
    count = 0;
    for (i = 0; i < size; i++)
        if (!marked[i]) count++;
    MPI_Reduce(&count, &global_count, 1, MPI_INT, MPI_SUM,
               0, MPI_COMM_WORLD);

    /* Stop the timer */

    elapsed_time += MPI_Wtime();

    /* Print the results */

    if (!id) {
        printf("There are %lld primes less than or equal to %lld\n",
               global_count, n);
        printf("SIEVE (%d) %10.6f\n", p, elapsed_time);
    }
    MPI_Finalize();
    return 0;
}

`optimize.cpp`

  
#include "mpi.h"
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define MIN(a, b) ((a) < (b) ? (a) : (b))
#define LL long long

int main(int argc, char *argv[]) {
    LL count;            /* Local prime count */
    double elapsed_time; /* Parallel execution time */
    LL first;            /* Index of first multiple */
    LL global_count = 0; /* Global prime count */
    LL high_value;       /* Highest value on this proc */
    LL i;
    int id;              /* Process ID number */
    LL index;            /* Index of current prime */
    LL low_value;        /* Lowest value on this proc */
    char *marked;        /* Portion of 2,...,'n' */
    LL n;                /* Sieving from 2, ..., 'n' */
    int p;               /* Number of processes */
    LL proc0_size;       /* Size of proc 0's subarray */
    LL prime;            /* Current prime */
    LL size;             /* Elements in 'marked' */

    MPI_Init(&argc, &argv);

    /* Start the timer */

    MPI_Comm_rank(MPI_COMM_WORLD, &id);
    MPI_Comm_size(MPI_COMM_WORLD, &p);
    MPI_Barrier(MPI_COMM_WORLD);
    elapsed_time = -MPI_Wtime();

    if (argc != 2) {
        if (!id)
            printf("Command line: %s <m>\n", argv[0]);
        MPI_Finalize();
        exit(1);
    }

    n = atoll(argv[1]);

    /* Figure out this process's share of the array, as
       well as the integers represented by the first and
       last array elements */

    low_value = 2 + id * (n - 1) / p;
    high_value = 1 + (id + 1) * (n - 1) / p;
    // 大小开一半就行
    size = (high_value - low_value) / 2 + 1;

    /* Bail out if all the primes used for sieving are
       not all held by process 0 */

    proc0_size = (n - 1) / p;

    if ((2 + proc0_size) < (int)sqrt((double)n)) {
        if (!id)
            printf("Too many processes\n");
        MPI_Finalize();
        exit(1);
    }

    /* Allocate this process's share of the array. */

    marked = (char *)malloc(size);

    if (marked == NULL) {
        printf("Cannot allocate enough memory\n");
        MPI_Finalize();
        exit(1);
    }

    for (i = 0; i < size; i++)
        marked[i] = 0;
    if (!id)
        index = 0;
    prime = 3;
    do {
        if (prime * prime > low_value)
            first = (prime * prime - low_value) / 2;
        else {
            if (!(low_value % prime))
                first = 0;
            else if (low_value % prime % 2 == 0)
                first = prime - ((low_value % prime) / 2);
            else
                first = (prime - (low_value % prime)) / 2;
        }
        for (i = first; i < size; i += prime)
            marked[i] = 1;
        if (!id) {
            while (marked[++index])
                ;
            prime = index * 2 + 3;
        }
        if (p > 1)
            MPI_Bcast(&prime, 1, MPI_INT, 0, MPI_COMM_WORLD);
    } while (prime * prime <= n);
    count = 0;
    for (i = 0; i < size; i++)
        if (!marked[i])
            count++;

    MPI_Reduce(&count, &global_count, 1, MPI_INT, MPI_SUM, 0, MPI_COMM_WORLD);
    global_count++;
    /* Stop the timer */

    elapsed_time += MPI_Wtime();

    /* Print the results */

    if (!id) {
        printf("There are %lld primes less than or equal to %lld\n", global_count,
               n);
        printf("SIEVE (%d) %10.6f\n", p, elapsed_time);
    }
    MPI_Finalize();
    return 0;
}

`optimize2.cpp`

  
#include "mpi.h"
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <vector>
using namespace std;
#define MIN(a, b) ((a) < (b) ? (a) : (b))
#define LL long long

int main(int argc, char *argv[]) {
    LL count;            /* Local prime count */
    double elapsed_time; /* Parallel execution time */
    LL first;            /* Index of first multiple */
    LL global_count = 0; /* Global prime count */
    LL high_value;       /* Highest value on this proc */
    LL i;
    int id;              /* Process ID number */
    LL index;            /* Index of current prime */
    LL low_value;        /* Lowest value on this proc */
    char *marked;        /* Portion of 2,...,'n' */
    LL n;                /* Sieving from 2, ..., 'n' */
    int p;               /* Number of processes */
    LL proc0_size;       /* Size of proc 0's subarray */
    LL prime;            /* Current prime */
    LL size;             /* Elements in 'marked' */

    MPI_Init(&argc, &argv);

    /* Start the timer */

    MPI_Comm_rank(MPI_COMM_WORLD, &id);
    MPI_Comm_size(MPI_COMM_WORLD, &p);
    MPI_Barrier(MPI_COMM_WORLD);
    elapsed_time = -MPI_Wtime();

    if (argc != 2) {
        if (!id)
            printf("Command line: %s <m>\n", argv[0]);
        MPI_Finalize();
        exit(1);
    }

    n = atoll(argv[1]);

    // 欧拉筛sqrt(n)内的质数
    vector<int> pri;
    int pri_i = 1;
    int sqrt_N = sqrt(n) + 10;
    bool not_prime[sqrt_N + 10] = {0};
    for (int i = 2; i <= sqrt_N; i++) {
        if (!not_prime[i]) pri.push_back(i);
        for (int prime_i : pri) {
            if (i * prime_i > sqrt_N) break;
            not_prime[i * prime_i] = true;
            if (i % prime_i == 0) break;
        }
    }

    /* Figure out this process's share of the array, as
       well as the integers represented by the first and
       last array elements */

    low_value = 2 + id * (n - 1) / p;
    high_value = 1 + (id + 1) * (n - 1) / p;
    // 大小开一半就行
    size = (high_value - low_value) / 2 + 1;

    /* Bail out if all the primes used for sieving are
       not all held by process 0 */

    proc0_size = (n - 1) / p;

    if ((2 + proc0_size) < (int)sqrt((double)n)) {
        if (!id)
            printf("Too many processes\n");
        MPI_Finalize();
        exit(1);
    }

    /* Allocate this process's share of the array. */

    marked = (char *)malloc(size);

    if (marked == NULL) {
        printf("Cannot allocate enough memory\n");
        MPI_Finalize();
        exit(1);
    }

    for (i = 0; i < size; i++)
        marked[i] = 0;
    if (!id)
        index = 0;
    prime = pri[pri_i];
    do {
        if (prime * prime > low_value)
            first = (prime * prime - low_value) / 2;
        else {
            if (!(low_value % prime))
                first = 0;
            else if (low_value % prime % 2 == 0) // 去除偶数
                first = prime - ((low_value % prime) / 2);
            else
                first = (prime - (low_value % prime)) / 2;
        }
        for (i = first; i < size; i += prime)
            marked[i] = 1;
        prime = pri[++pri_i];
    } while (prime * prime <= n);
    count = 0;
    for (i = 0; i < size; i++)
        if (!marked[i])
            count++;

    MPI_Reduce(&count, &global_count, 1, MPI_INT, MPI_SUM, 0, MPI_COMM_WORLD);
    global_count++;
    /* Stop the timer */

    elapsed_time += MPI_Wtime();

    /* Print the results */

    if (!id) {
        printf("There are %lld primes less than or equal to %lld\n", global_count,
               n);
        printf("SIEVE (%d) %10.6f\n", p, elapsed_time);
    }
    MPI_Finalize();
    return 0;
}

`optimize3.cpp`

  
#include "mpi.h"
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <vector>
using namespace std;
#define MIN(a, b) ((a) < (b) ? (a) : (b))
#define LL long long
#define CACHE_SIZE 33554432
#define CACHELINE_SIZE 64

int main(int argc, char *argv[]) {
    LL count;            /* Local prime count */
    double elapsed_time; /* Parallel execution time */
    LL first;            /* Index of first multiple */
    LL global_count = 0; /* Global prime count */
    LL high_value;       /* Highest value on this proc */
    LL i;
    int id;              /* Process ID number */
    LL index;            /* Index of current prime */
    LL low_value;        /* Lowest value on this proc */
    char *marked;        /* Portion of 2,...,'n' */
    LL n;                /* Sieving from 2, ..., 'n' */
    int p;               /* Number of processes */
    LL proc0_size;       /* Size of proc 0's subarray */
    LL prime;            /* Current prime */
    LL size;             /* Elements in 'marked' */

    MPI_Init(&argc, &argv);

    /* Start the timer */

    MPI_Comm_rank(MPI_COMM_WORLD, &id);
    MPI_Comm_size(MPI_COMM_WORLD, &p);
    MPI_Barrier(MPI_COMM_WORLD);
    elapsed_time = -MPI_Wtime();

    if (argc != 2) {
        if (!id)
            printf("Command line: %s <m>\n", argv[0]);
        MPI_Finalize();
        exit(1);
    }

    n = atoll(argv[1]);

    // 欧拉筛sqrt(n)内的质数
    vector<int> pri;
    int pri_i = 1;
    int sqrt_N = sqrt(n) + 10;
    bool not_prime[sqrt_N + 10] = {0};
    for (int i = 2; i <= sqrt_N; i++) {
        if (!not_prime[i]) pri.push_back(i);
        for (int prime_i : pri) {
            if (i * prime_i > sqrt_N) break;
            not_prime[i * prime_i] = true;
            if (i % prime_i == 0) break;
        }
    }

    /* Figure out this process's share of the array, as
       well as the integers represented by the first and
       last array elements */
    LL N = (n - 1) / 2;
    LL low_index = id * (N / p) + MIN(id, N % p); // 该进程的第一个数的索引
    LL high_index = (id + 1) * (N / p) + MIN(id + 1, N % p) - 1;
    low_value = low_index * 2 + 3;
    high_value = (high_index + 1) * 2 + 1;

    size = (high_value - low_value) / 2 + 1;

    /* Bail out if all the primes used for sieving are
       not all held by process 0 */

    proc0_size = (n - 1) / p;

    if ((2 + proc0_size) < (int)sqrt((double)n)) {
        if (!id)
            printf("Too many processes\n");
        MPI_Finalize();
        exit(1);
    }

    /* Allocate this process's share of the array. */
    //

    int CacheBlock_size = (CACHE_SIZE / p) >> 4;
    int Block_need = size / CacheBlock_size;
    int Block_rest = size % CacheBlock_size;
    int Block_id = 0;
    int Block_N = CacheBlock_size - 1;
    LL Block_low_value, Block_high_value, Block_first, Block_last;
    LL count_cacheBlock;

    marked = (char *)malloc(CacheBlock_size);

    if (marked == NULL) {
        printf("Cannot allocate enough memory\n");
        MPI_Finalize();
        exit(1);
    }

    count = 0;
    while (Block_id <= Block_need) {
        // 更新Cache
        Block_first = Block_id * Block_N + MIN(Block_id, Block_rest) + low_index;
        Block_last = (Block_id + 1) * Block_N + MIN(Block_id + 1, Block_rest) - 1 + low_index;
        Block_low_value = 2 * Block_first + 3;
        if (Block_id == Block_need) {
            Block_high_value = high_value;
            Block_last = high_index;
            CacheBlock_size = (Block_high_value - Block_low_value) / 2 + 1;
        } else {
            Block_high_value = 2 * Block_last + 3;
        }

        pri_i = 1;
        prime = pri[pri_i];
        count_cacheBlock = 0;
        for (int i = 0; i < CacheBlock_size; i++) marked[i] = 0;

        do {
            if (prime * prime > Block_low_value)
                first = (prime * prime - Block_low_value) / 2;
            else {
                if (!(Block_low_value % prime))
                    first = 0;
                else if (Block_low_value % prime % 2 == 0)
                    first = prime - (Block_low_value % prime) / 2;
                else
                    first = (prime - (Block_low_value % prime)) / 2;
            }
            for (i = first; i < CacheBlock_size; i += prime)
                marked[i] = 1;

            prime = pri[++pri_i];
        } while (prime * prime <= Block_high_value);

        for (i = 0; i < CacheBlock_size; i++)
            if (!marked[i])
                count_cacheBlock++;

        count += count_cacheBlock;
        Block_id++;
    }

    MPI_Reduce(&count, &global_count, 1, MPI_INT, MPI_SUM, 0, MPI_COMM_WORLD);
    global_count++;
    /* Stop the timer */

    elapsed_time += MPI_Wtime();

    /* Print the results */

    if (!id) {
        printf("There are %lld primes less than or equal to %lld\n", global_count,
               n);
        printf("SIEVE (%d) %10.6f\n", p, elapsed_time);
    }
    MPI_Finalize();
    return 0;
}

`optimize4.cpp`

  
#include "mpi.h"
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <vector>
#include <cstring>
using namespace std;
#define MIN(a, b) ((a) < (b) ? (a) : (b))
#define LL long long
#define CACHE_SIZE 33554432
#define likely(x) __builtin_expect(!!(x), 1)
#define unlikely(x) __builtin_expect(!!(x), 0)

int main(int argc, char *argv[]) {
    LL count = 0;           /* Local prime count */
    double elapsed_time;    /* Parallel execution time */
    register LL first;      /* Index of first multiple */
    LL global_count = 0;    /* Global prime count */
    register LL high_value; /* Highest value on this proc */
    register LL i;
    register int id;        /* Process ID number */
    LL index;               /* Index of current prime */
    LL low_value;           /* Lowest value on this proc */
    register bool *marked;  /* Portion of 2,...,'n' */
    register bool *mark;
    LL n;                   /* Sieving from 2, ..., 'n' */
    int p;                  /* Number of processes */
    LL proc0_size;          /* Size of proc 0's subarray */
    register LL prime;      /* Current prime */
    LL size;                /* Elements in 'marked' */
    register LL Block_low_value, Block_high_value, Block_first, Block_last;
    register LL prime_square;
    register LL tmpSize; // 用来循环计数的，防止越界
    register LL tmpPrime;
    register LL count_cacheBlock0 = 0, count_cacheBlock1 = 0, count_cacheBlock2 = 0, count_cacheBlock3 = 0, count_cacheBlock4 = 0, count_cacheBlock5 = 0, count_cacheBlock6 = 0, count_cacheBlock7 = 0;

    register bool *tmp_marked asm("x7");
    register unsigned LL tmp_i asm("x9");
    register unsigned LL tmp_prime asm("x10");
    register unsigned int zero asm("w8");

    MPI_Init(&argc, &argv);

    /* Start the timer */

    MPI_Comm_rank(MPI_COMM_WORLD, &id);
    MPI_Comm_size(MPI_COMM_WORLD, &p);
    MPI_Barrier(MPI_COMM_WORLD);
    elapsed_time = -MPI_Wtime();

    if (argc != 2) {
        if (!id)
            printf("Command line: %s <m>\n", argv[0]);
        MPI_Finalize();
        exit(1);
    }

    n = atoll(argv[1]);

    // 欧拉筛sqrt(n)内的质数

    register vector<int> pri;
    int pri_i = 1;
    register int sqrt_N = sqrt(n) + 10;
    register bool not_prime[sqrt_N + 10] = {0};
    for (register int i = 2; i <= sqrt_N; i++) {
        if (!not_prime[i]) pri.emplace_back(i);
        for (register int prime_i : pri) {
            if (i * prime_i > sqrt_N) break;
            not_prime[i * prime_i] = true;
            if (i % prime_i == 0) break;
        }
    }

    /* Figure out this process's share of the array, as
       well as the integers represented by the first and
       last array elements */
    LL N = (n - 1) >> 1;
    register LL low_index = id * (N / p) + MIN(id, N % p); // 该进程的第一个数的索引
    LL high_index = (id + 1) * (N / p) + MIN(id + 1, N % p) - 1;
    low_value = (low_index << 1) + 3;
    high_value = ((high_index + 1) << 1) + 1;
    size = ((high_value - low_value) >> 1) + 1;

    /* Bail out if all the primes used for sieving are
       not all held by process 0 */

    proc0_size = (n - 1) / p;

    if ((2 + proc0_size) < (int)sqrt((double)n)) {
        if (!id)
            printf("Too many processes\n");
        MPI_Finalize();
        exit(1);
    }

    /* Allocate this process's share of the array. */
    //

    int CacheBlock_size = (CACHE_SIZE / p) >> 4;
    register int Block_need = size / CacheBlock_size;
    register int Block_rest = size % CacheBlock_size;
    register int Block_id = 0;
    register int Block_N = CacheBlock_size - 1;
    register int BlocLowModPrime;
    marked = (bool *)malloc(CacheBlock_size);

    if (marked == NULL) {
        printf("Cannot allocate enough memory\n");
        MPI_Finalize();
        exit(1);
    }

    while (Block_id <= Block_need) {
        pri_i = 1;
        prime = 3;
        prime_square = prime * prime;
        memset(marked, 1, CacheBlock_size);
        count_cacheBlock0 = 0, count_cacheBlock1 = 0, count_cacheBlock2 = 0, count_cacheBlock3 = 0, count_cacheBlock4 = 0, count_cacheBlock5 = 0, count_cacheBlock6 = 0, count_cacheBlock7 = 0;
        // 更新Cache
        Block_first = Block_id * Block_N + MIN(Block_id, Block_rest) + low_index;
        Block_last = (Block_id + 1) * Block_N + MIN(Block_id + 1, Block_rest) - 1 + low_index;
        Block_low_value = (Block_first << 1) + 3;
        if (unlikely(Block_id == Block_need)) {
            Block_high_value = high_value;
            Block_last = high_index;
            CacheBlock_size = ((Block_high_value - Block_low_value) >> 1) + 1;
        } else {
            Block_high_value = (Block_last << 1) + 3;
        }

        do {
            BlocLowModPrime = Block_low_value % prime;
            if (unlikely(prime_square > Block_low_value))
                first = (prime_square - Block_low_value) >> 1;
            else {
                if (unlikely(BlocLowModPrime == 0))
                    first = 0;
                else {
                    first = ((BlocLowModPrime & 1) == 0) ?
                                (prime - (BlocLowModPrime >> 1)) :
                                (prime - BlocLowModPrime) >> 1;
                }
            }

            tmpSize = CacheBlock_size - (CacheBlock_size - first) % (prime << 3);
            i = first;
            tmp_marked = &marked[0];        // x7
            tmp_i = (unsigned LL)i;         // x9
            tmp_prime = (unsigned LL)prime; // x10
            zero = 0;                       // w8
            asm volatile(
                "2:\n"
                "cmp x9, %2\n"       // i < tmpSize?
                "bge 1f\n"
                "strb w8, [x7,x9]\n" // marked[i] = 0
                "adds x9, x9, x10\n" // i+=prime
                "strb w8, [x7,x9]\n"
                "adds x9, x9, x10\n"
                "strb w8, [x7,x9]\n"
                "adds x9, x9, x10\n"
                "strb w8, [x7,x9]\n"
                "adds x9, x9, x10\n"
                "strb w8, [x7,x9]\n"
                "adds x9, x9, x10\n"
                "strb w8, [x7,x9]\n"
                "adds x9, x9, x10\n"
                "strb w8, [x7,x9]\n"
                "adds x9, x9, x10\n"
                "strb w8, [x7,x9]\n"
                "adds x9, x9, x10\n"
                "b 2b\n"
                "1:\n"
                : "+r"(tmp_i)
                : "r"(tmp_marked), "r"(tmpSize), "r"(zero)
                : "cc", "memory");
            i = tmp_i;
            for (; i < CacheBlock_size; i += prime) marked[i] = 0;

            prime = pri[++pri_i];
            prime_square = prime * prime;
        } while (prime_square <= Block_high_value);

        tmpSize = (CacheBlock_size >> 6) << 6;
        for (i = 0; i < tmpSize; i += 64) {
            mark = marked + i;
            count_cacheBlock0 += __builtin_popcountll(*((unsigned long long *)(mark)));
            count_cacheBlock1 += __builtin_popcountll(*((unsigned long long *)(mark + 8)));
            count_cacheBlock2 += __builtin_popcountll(*((unsigned long long *)(mark + 16)));
            count_cacheBlock3 += __builtin_popcountll(*((unsigned long long *)(mark + 24)));
            count_cacheBlock4 += __builtin_popcountll(*((unsigned long long *)(mark + 32)));
            count_cacheBlock5 += __builtin_popcountll(*((unsigned long long *)(mark + 40)));
            count_cacheBlock6 += __builtin_popcountll(*((unsigned long long *)(mark + 48)));
            count_cacheBlock7 += __builtin_popcountll(*((unsigned long long *)(mark + 56)));
        }
        count += count_cacheBlock0 + count_cacheBlock1 + count_cacheBlock2 + count_cacheBlock3 + count_cacheBlock4 + count_cacheBlock5 + count_cacheBlock6 + count_cacheBlock7;
        for (; i < CacheBlock_size; i++) count += marked[i];

        Block_id++;
    }

    MPI_Reduce(&count, &global_count, 1, MPI_INT, MPI_SUM, 0, MPI_COMM_WORLD);
    global_count++;

    /* Stop the timer */

    elapsed_time += MPI_Wtime();

    /* Print the results */

    if (!id) {
        printf("There are %lld primes less than or equal to %lld\n", global_count,
               n);
        printf("SIEVE (%d) %10.6f\n", p, elapsed_time);
    }
    MPI_Finalize();
    return 0;
}

Study, MPI

MPI

This post is licensed under CC BY 4.0 by the author.

并行计算MPI 埃拉筛及性能优化

埃拉托斯特尼素数筛选算法并行及性能优化

实验目的

实验环境

实验过程

$\boxed{\text{base}}$：普通的 MPI 埃拉筛

`base.cpp` 程序框图：

`base.cpp` 程序运行结果：

$\boxed{\text{optimize1}}$：去除偶数

`optimize1.cpp` 程序框图：

`optimize1.cpp` 运行结果：

$\boxed{\text{optimize2}}$：消除广播

`optimize2.cpp` 程序框图：

`optimize2.cpp` 运行结果：

$\boxed{\text{optimize3}}$ Cache 优化

`optimize3.cpp` 程序框图：

`optimize3.cpp` 运行结果：

$\boxed{\text{optimize4}}$ 最终优化

使用 `memset` 替换 `for` 循环初始化 `marked` 数组

循环展开

使用 `__builtin_popcountll` 函数来统计

继续减少标记 `marked` 数组部分的分支判断

增加标记 `marked` 数组的循环展开常数

杂七杂八的优化

使用 `register` 关键字 & 内联汇编

`optimize4.cpp` 运行结果：

代码

`base.cpp`

`optimize.cpp`

`optimize2.cpp`

`optimize3.cpp`

`optimize4.cpp`

Trending Tags

埃拉托斯特尼素数筛选算法并行及性能优化

实验目的

实验环境

实验过程

$\boxed{\text{base}}$：普通的 MPI 埃拉筛

base.cpp 程序框图：

base.cpp 程序运行结果：

$\boxed{\text{optimize1}}$：去除偶数

optimize1.cpp 程序框图：

optimize1.cpp 运行结果：

$\boxed{\text{optimize2}}$：消除广播

optimize2.cpp 程序框图：

optimize2.cpp 运行结果：

$\boxed{\text{optimize3}}$ Cache 优化

optimize3.cpp 程序框图：

optimize3.cpp 运行结果：

$\boxed{\text{optimize4}}$ 最终优化

使用 memset 替换 for 循环初始化 marked 数组

循环展开

使用 __builtin_popcountll 函数来统计

继续减少标记 marked 数组部分的分支判断

增加标记 marked 数组的循环展开常数

杂七杂八的优化

使用 register 关键字 & 内联汇编

optimize4.cpp 运行结果：

代码

base.cpp

optimize.cpp

optimize2.cpp

optimize3.cpp

optimize4.cpp

Trending Tags

`base.cpp` 程序框图：

`base.cpp` 程序运行结果：

`optimize1.cpp` 程序框图：

`optimize1.cpp` 运行结果：

`optimize2.cpp` 程序框图：

`optimize2.cpp` 运行结果：

`optimize3.cpp` 程序框图：

`optimize3.cpp` 运行结果：

使用 `memset` 替换 `for` 循环初始化 `marked` 数组

使用 `__builtin_popcountll` 函数来统计

继续减少标记 `marked` 数组部分的分支判断

增加标记 `marked` 数组的循环展开常数

使用 `register` 关键字 & 内联汇编

`optimize4.cpp` 运行结果：

`base.cpp`

`optimize.cpp`

`optimize2.cpp`

`optimize3.cpp`

`optimize4.cpp`